随着教育普及化的进程，越来越多的人选择通过专升本的方式提升自己的学历，高等数学作为专升本考试的必考科目，其重要性不言而喻，掌握高等数学中的关键公式，对于备考和解决实际问题都具有重要意义，本文将详细介绍一些在专升本高等数学中常用的公式，帮助考生更好地理解和掌握高等数学的知识。

函数与极限

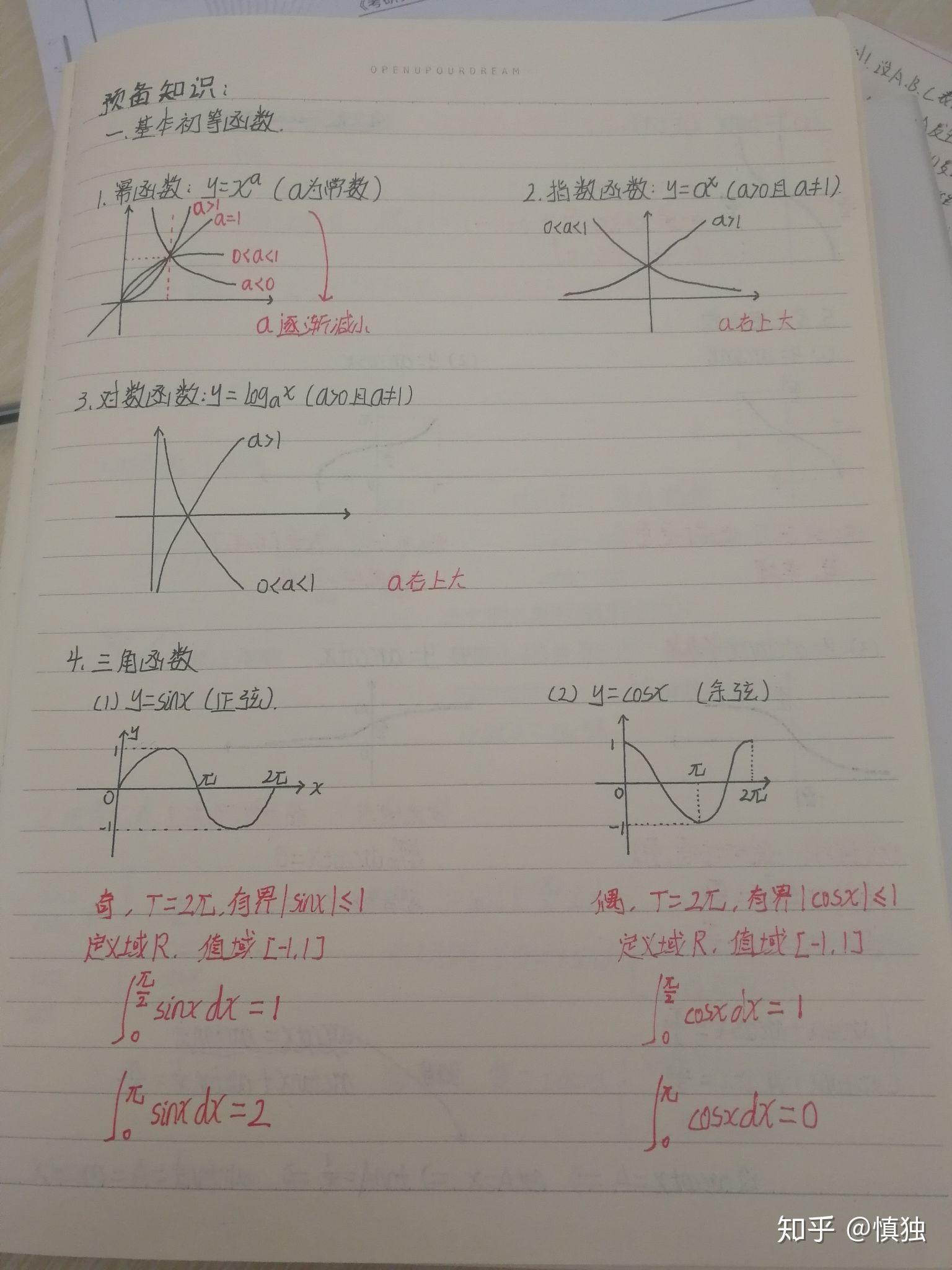
1、函数基本公式：y=f(x)，了解函数的概念、性质和类型，是学习数学的基础。

2、极限公式：lim(x→a) f(x) = L，极限是高等数学的重要概念，掌握极限的计算方法和应用，对于后续学习至关重要。

微积分

1、导数公式：导数描述了函数在某一点的切线斜率，常用导数公式包括基本初等函数的导数公式、导数的四则运算法则等。

2、积分公式：积分用于计算函数在一定区间上的面积或体积，常用的积分公式包括不定积分和定积分的计算法则。

3、微分方程：描述自然现象中量与量之间的变化规律，掌握常见微分方程的求解方法，如分离变量法、一阶线性微分方程等。

空间解析几何

1、空间向量公式：向量的概念在解析几何中占有重要地位，掌握向量的基本运算、向量积、向量投影等公式，有助于解决空间几何问题。

2、空间曲面方程：常见的空间曲面方程包括平面方程、球面方程、柱面方程等，了解这些方程的形式和性质，对于解决空间几何问题非常有帮助。

级数与序列

1、级数求和公式：级数求和是高等数学中的重要内容，掌握等差数列和等比数列的求和公式，以及无穷级数的敛散性判断方法。

2、序列极限：了解序列极限的概念和性质，掌握判断序列极限的方法，对于解决数学问题具有重要意义。

多元函数与积分学

1、偏导数公式：偏导数描述了一个多元函数在某一点上关于一个变量的变化率，掌握偏导数的计算方法和应用，对于解决实际问题非常重要。

2、多元函数积分学：包括二重积分、三重积分、曲线积分和曲面积分等，这些积分公式在解决实际问题中广泛应用，掌握其计算方法和应用技巧至关重要。

专升本高等数学涉及的知识点众多，掌握常用公式对于备考和解决实际问题具有重要意义，本文介绍了函数与极限、微积分、空间解析几何、级数与序列以及多元函数与积分学等方面的常用公式，考生在学习过程中，应注重理解公式的推导过程和应用场景，通过不断练习巩固所学知识，要注意将理论知识与实际问题相结合，培养解决实际问题的能力。

建议学习方法

1、制定学习计划：明确学习目标，合理安排学习时间，做到有的放矢。

2、掌握基础知识：从基础知识入手，逐步深入学习高等数学的相关知识。

3、多做练习：通过大量练习，巩固所学知识，提高解题能力。

4、寻求帮助：遇到难题时，及时向老师、同学请教，或查阅相关资料。

希望本文能对专升本高等数学的学习者有所帮助，掌握高等数学中的常用公式，将有助于考生更好地备考和解决实际问题。